符号表
符号表的主要目的是将一个键和一个值联系起来,可以根据键获得值。我们会用多种方式实现这种数据结构,不仅能高效的插入和查找,还可以进行其他方便的操作。这里我们还会讨论java中符号表的实现。为了熟悉kotlin这里所有的算法都将使用kotlin来实现。
规则
- 每个键对应一个值
- 键值均不允许null(java中hashmap是可以为空的)
- 删除操作,有延时删除(先置空再删除)和即时删除(直接删除)
- 迭代,便利所有键
- 键的等价性,equals判断是否相等,如果使用了comparable接口来进行比较,那么保证equals与compareTo返回值一致。
总有人问hashmap是否有序,hashmap在使用时对键没有要求,不需要实现接口Iterable,也就是说键无法比较,那么怎么可能是有序的呢
基于无序链表的顺序查找
基于链表的实现,在查找时只能是顺序查找1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57//kt中泛型的使用
class Search<Key : Comparable<Key>,Value>{
//如果可能为null,则需要加?修饰
private var first: Node? = null
private var N: Int = 0
fun put(key: Key,value: Value){
var x:Node? = first
while (x != null){
if (x.key!!.compareTo(key) == 0){
x.value = value
return
}else x = x.next
}
this.first = Node(key,value, first)
N++
}
//返回值有可能为null也需要加?修饰
fun get(key: Key): Value?{
var tmp = first
while (tmp != null){
if (tmp.key!!.compareTo(key) == 0) return tmp.value
tmp = tmp.next
}
return null
}
fun delete(key:Key){
if (first == null){
return
}
if (first?.key?.compareTo(key) == 0) {
first = first?.next
N--
return
}
var tmp = first
var pre : Node? = null
while (tmp != null){
if (tmp.key.compareTo(key) == 0){
pre?.next = tmp.next
N--
return
}else{
pre = tmp
tmp = tmp.next
}
}
}
fun size(): Int {
return N
}
//内部类,还有嵌套类,有区别,构造函数在类声明后面
inner class Node(val key: Key, var value: Value, var next: Node?)
}
基于无序链表的查找,未命中的查找和插入操作都需要N次比较。向一个空表中连续插入N个键需要$~\frac{N^2}{2}$次比较。所以基于无需链表的实现效率很低。
基于有序数组的二分查找
1 | class BinarySearch(var N: Int){ |
二分查找很快,在N个键的有序数组中进行二分查找最多需要(lgN+1)次比较(无论是否成功)。插入一个新元素在最坏的情况下要访问数组~2N次,因此向一个空符号表中插入N个元素在最坏情况下需要访问$~N^2$次数组。也就是说,基于有序数组实现的符号表插入效率低下,这是一个缺陷。
基于链表和有序数组的符号表实现比较

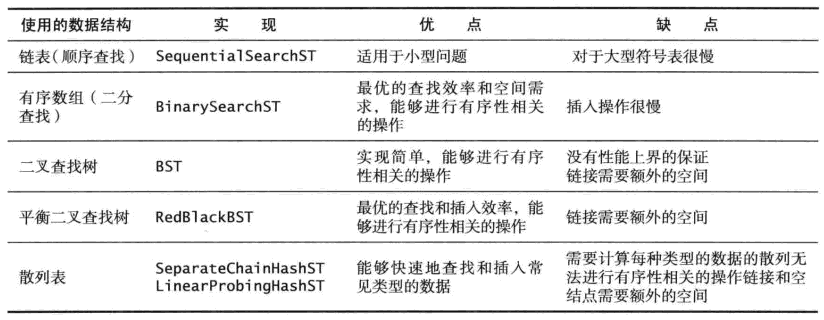
二叉查找树
要支持高效的插入操作,需要支持二分查找的链式结构,但单链表显然无法满足,因为二分查找的高效来自于可以通过索引快速的入得任何数组的中间元素,但得到链表中间元素的唯一方法就是遍历。将二分查找和链表的灵活性结合起来,我们需要更复杂的数据结构,就是二叉查找树。
二叉树
在计算机科学中,二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
二叉树的根结点所在的层数为1,根结点的孩子结点所在的层数为2,以此下去。深度是指所有结点中最深的结点所在的层数。
二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有2^{i-1}个结点;深度为k的二叉树至多有2^k-1个结点;对任何一棵二叉树T,如果其叶子结点数为n_0,度为2的结点数为n_2,则n_0=n_2+1。
一棵深度为k,且有2^k-1个节点的二叉树,称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树。具有n个节点的完全二叉树的深度为log2n+1。深度为k的完全二叉树,至少有2^(k-1)个节点,至多有2^k-1个节点。
二叉树是递归定义的,其结点有左右子树之分,逻辑上二叉树有五种基本形态:
(1)空二叉树
(2)只有一个根结点的二叉树
(3)只有左子树
(4)只有右子树
(5)完全二叉树
注意:尽管二叉树与树有许多相似之处,但二叉树不是树的特殊情形。
二叉树类型
- 完全二叉树
- 满二叉树
- 平衡二叉树——平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
相关术语
树的结点:包含一个数据元素及若干指向子树的分支;
孩子结点:结点的子树的根称为该结点的孩子;
双亲结点:B 结点是A 结点的孩子,则A结点是B 结点的双亲;
兄弟结点:同一双亲的孩子结点; 堂兄结点:同一层上结点;
祖先结点: 从根到该结点的所经分支上的所有结点;
子孙结点:以某结点为根的子树中任一结点都称为该结点的子孙;
结点层:根结点的层定义为1;根的孩子为第二层结点,依此类推;
树的深度:树中最大的结点层
结点的度:结点子树的个数
树的度: 树中最大的结点度。
叶子结点:也叫终端结点,是度为 0 的结点;
分枝结点:度不为0的结点;
有序树:子树有序的树,如:家族树;
无序树:不考虑子树的顺序;遍历顺序
遍历是对树的一种最基本的运算,所谓遍历二叉树,就是按一定的规则和顺序走遍二叉树的所有结点,使每一个结点都被访问一次,而且只被访问一次。由于二叉树是非线性结构,因此,树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。
设L、D、R分别表示遍历左子树、访问根结点和遍历右子树, 则对一棵二叉树的遍历有三种情况:DLR(称为先根次序遍历),LDR(称为中根次序遍历),LRD (称为后根次序遍历)。
如何记忆三种遍历:
注意,DLR是先根次序遍历,即判断先中后的方式是看何时访问双亲节点,而LR永远都是先左后右的顺序。二叉树实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230package com.zgq;
public class BST <Key extends Comparable<Key>,Value>{
private Node root;
private class Node{
private Key key;
private Value value;
private int N;
private Node left,right;
private Node(Key key,Value value,int N){
this.key = key;
this.value = value;
this.N = N;
}
}
public void put(Key key, Value value){
root = put(root,key,value);
}
private Node put(Node root,Key key,Value value){
if (root == null){
return new Node(key,value,1);
}
int cmp = key.compareTo(root.key);
if (cmp > 0){
root.right = put(root.right,key,value);
}else if (cmp < 0){
root.left = put(root.left,key,value);
}else {
root.value = value;
}
root.N = sizeOf(root.left) + sizeOf(root.right) + 1;
return root;
}
public Value get(Key key){
return get(root,key);
}
private Value get(Node root, Key key){
if (root == null) return null;
int cmp = key.compareTo(root.key);
if (cmp > 0) return get(root.right,key);
else if (cmp < 0) return get(root.left,key);
else return root.value;
}
public int size(){
return sizeOf(root);
}
private int sizeOf(Node root){
if (root == null) return 0;
return root.N;
}
public Value max(){
return max(root).value;
}
private Node max(Node root){
if (root == null) return null;
if (root.right == null) return root;
return max(root.right);
}
public Value min(){
return min(root).value;
}
private Node min(Node root){
if (root == null) return null;
if (root.left == null) return root;
return min(root.left);
}
public void delete(Key key){
delete(root,key);
}
//删除节点并返回根节点
private Node delete(Node root,Key key){
if (root == null) return null;
int cmp = key.compareTo(root.key);
//在右子树中进行删除,同时保证root的右节点指向删除后得根节点
if (cmp > 0) root.right = delete(root.right,key);
else if (cmp < 0) root.left = delete(root.left,key);
else {
//如果找到节点,则分步删除
//左子树为空,则返回右子树根节点
if (root.left == null) return root.right;
//右子树为空,则返回左子树根节点
if (root.right == null) return root.left;
//左右都不为空,则将右子树中最小的节点copy到要删除节点root的位置,同时新root的左子树链接原root的左子树,新root的右子树链接删除最小节点后得右子树
Node t = root;
root = min(root.right);
root.left = t.left;
root.right = deleteMin(root.right);
}
root.N = sizeOf(root.left) + sizeOf(root.right) + 1;
return root;
}
public void deleteMin(){
root = deleteMin(root);
}
private Node deleteMin(Node root){
if (root.left == null) return root.right;
root.left = deleteMin(root.left);
root.N = sizeOf(root.left) + sizeOf(root.right) + 1;
return root;
}
public void deleteMax(){
root = deleteMax(root);
}
//删除最大节点并返回根节点
private Node deleteMax(Node root){
if (root.right == null) return root.left;
//递归实现
root.right = deleteMax(root.right);
root.N = sizeOf(root.left) + sizeOf(root.right) + 1;
return root;
}
public Key floor(Key key){
return floor(root,key).key;
}
private Node floor(Node root, Key key){
if (root == null) return null;
int cmp = key.compareTo(root.key);
if (cmp == 0) return root;
else if (cmp < 0) {
return floor(root.left, key);
}
Node t = floor(root.right,key);
if (t != null) return t;
else return root;
}
public Key ceiling(Key key){
return ceiling(root,key).key;
}
private Node ceiling(Node root, Key key){
if (root == null) return null;
int cmp = key.compareTo(root.key);
if (cmp == 0) return root;
else if (cmp > 0) {
return ceiling(root.right, key);
}
Node t = ceiling(root.left,key);
if (t != null) return t;
else return root;
}
//返回比key小的节点数量
public int rank(Key key){
return rank(root,key);
}
private int rank(Node root, Key key){
if (root == null) return 0;
int cmp = key.compareTo(root.key);
if (cmp < 0) return rank(root.left,key);
//注意这里,当key比root节点大时,返回root的子节点数量+对root右子树做rank操作的结果+1
else if (cmp > 0) return 1 + sizeOf(root.left) + rank(root.right,key);
else return sizeOf(root.left);
}
//返回排名为k的元素,从0开始排
public Key select(int k){
return select(root,k).key;
}
private Node select(Node root, int k){
if (root == null) return null;
int t = sizeOf(root.left);
if (t < k) return select(root.right,k-t-1);
else if (t > k) return select(root.left,k);
else return root;
}
//范围查找操作
//返回所有键,无序
public Iterable<Key> keys(){
return keys(min(),max());
}
//返回lo到hi之间的所有键
public Iterable<Key> keys(Key lo,Key hi){
Queue<Key> queue = new ArrayBlockingQueue<>(10);
keys(root,queue,lo,hi);
return queue;
}
private void keys(Node root, Queue<Key> queue,Key lo,Key hi){
if (root == null) return;
int cmpLo = lo.compareTo(root.key);
int cmpHi = hi.compareTo(root.key);
if (cmpLo <= 0 && cmpHi >= 0){
queue.add(root.key);
}
if (cmpLo < 0){
keys(root.left,queue,lo,hi);
}
if (cmpHi > 0){
keys(root.right,queue,lo,hi);
}
}
public void printAllLDR(){
printAllLDR(root);
System.out.print("\n");
}
private void printAllLDR(Node root){
if (root.left != null) {
printAllLDR(root.left);
}
System.out.print("*" + root.key + "*");
if (root.right != null) {
printAllLDR(root.right);
}
}
}
使用二叉查找树的算法运算时间取决于树的形状,而树的形状右取决于键被插入的先后顺序。在最好的情况下,N个节点的数是完全平衡的,每条空链到根节点的距离都是lgN。但是在最坏的情况下,搜索路径上可能有N个节点。
二叉查找树和快排有极高的相似度,根节点就是快排的切分元素。
性质
- 在由N个随机键构造的二叉查找树中,查找命中平均所需比较次数~2lgN(约1.39lgN)。
- 在由N个随机键构造的二叉查找树中,插入操作和查找未命中平均所需比较次数~2lgN(约1.39lgN)。
性能分析
- 在一棵二叉查找树中,所有操作在最坏情况下所需时间都和树的高度成正比。
- 二叉树的优势还在于其支持高效的rank(),select(),delete()以及范围查找操作。
- 某些最坏的情况下仍有恶劣的性能。
平衡查找树
在一个含有N个节点的树中,我们希望树高为lgN,这样就能保证每次查找都能在树高次比较中结束,就像二分查找一样。但是在动态插入中保证树的完美平衡代价很大,这节将要解决这个问题。23查找树
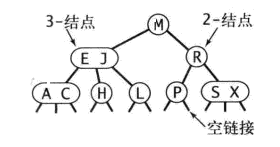
一颗完美平衡的23查找树中的所有空节点到根节点的距离都是相同的 - 查找,与二叉树类似
- 插入:插入操作较为麻烦,在二叉树中插入时,我们是先做一个查找,如果未命中,则把新节点挂在树的底部,这样的影响是树无法保证完美平衡性。使用23树可以避免这种情况。
插入过程详解
- 未命中查找结束与一个2节点,把2节点转换成3节点,再将新节点保存在其中即可。
- 树中只含有3节点,