sort-algorithm

选择排序

一般用于小型数组

public static void selection(Comparable[] a){
    for (int i = 0; i < a.length; i++){
        int min = i;
        for (int j = i + 1 ; j < a.length; j++){
            if (a[min].compareTo(a[j]) > 0){
                min = j;
            }
        }
        exch(a,min,i);
    }
}

插入排序

一般用于小型数组

public static void insertion(Comparable[] a){
    for (int i = 0; i < a.length - 1; i++){
        for (int j = i ; j > 0 && a[j-1].compareTo(a[j]) > 0 ; j--){
            exch(a,j-1,j);
        }
    }
}

希尔排序

内循环是插入排序，第一个for循环相当于完成了所有h有序数组的插入排序。比较顺序是：

1. 第一个h有序数组的前一位插入排序
2. 第二个h有序数组的前一位插入排序直到第h个有序数组的前一位插入排序
3. 第一个h有序数组的前两位插入排序直到第h个有序数组的前两位插入排序
4. 同理，直到第h个有序数组的所有位数插入排序

下面程序中的h不断减小直到为1，这个时候数组就是有序的了。
这个程序中，h = 3*h +1,即1，4，13·····，这个序列叫递增序列，递增序列的选择有很多，可以在运行时计算得到，也可以保存在数组中。递增序列的选择会直接影响希尔排序的性能，在普通情况下，h = 3*h +1足够满足我们。
希尔排序的优势在于可以处理中型数组，且不会占用额外的空间。
希尔排序与选择排序和插入排序相比，希尔排序也可以用于大型数组。

public static void shell(Comparable[] a){
    int h = 1;
    int N = a.length;
    while(h < N/3) h = h*3 + 1;
    while (h>=1) {
        for (int i = h; i < N; i++) {
            for (int j = i; j >= h && a[j].compareTo(a[j-h]) < 0; j -= h)
                exch(a,j,j-h);
        }
        h = h/3;
    }
}

归并排序

归并排序，时间复杂度为NlogN，它的主要缺点是需要额外空间，切额外空间的大小与N成正比。

public class Merge {

    private static Comparable[] aux;

    public static void sort(Comparable[] a){
        aux = new Comparable[a.length];
        sort(a, 0, a.length - 1);
    }
    //自顶向下递归进行归并排序
    private static void sort(Comparable[] a, int lo, int hi){
        if (hi <= lo) return;
        sort(a,lo,lo + (hi - lo)/2);
        sort(a,lo + (hi - lo)/2 + 1,hi);
        merge(a,lo,hi,lo + (hi - lo)/2);
    }
    //归并方法
    private static void merge(Comparable[] a, int lo, int hi, int mid){
        for (int i = lo; i <= hi; i++){
            aux[i] = a[i];
        }
        int i = lo;
        int j = mid + 1;
        for (int k = lo; k <= hi; k++){
            if (j > hi) a[k] = aux[i++];
            else if (i > mid) a[k] = aux[j++];
            else if (aux[i].compareTo(aux[j])>=0) a[k] = aux[j++];
            else if (aux[i].compareTo(aux[j])<0) a[k] = aux[i++];
        }
    }
}

归并排序的优化

1. 对于小规模的数组不再递归，而使用简单的选择排序或者插入排序，因为这两种排序在小规模数组上速度很可能比归并快，一般情况下可以将归并排序缩短10%到15%。
   在子数组长度小于一定值时（这里是4），使用插入排序。

   private static void sort(Comparable[] a, int lo, int hi){
       if (hi <= lo) return;
       if ((hi - lo) < 4){
           insertion(a, lo, hi);
           return;
       }
       sort(a,lo,lo + (hi - lo)/2);
       sort(a,lo + (hi - lo)/2 + 1,hi);
       merge(a,lo,hi,lo + (hi - lo)/2);
   }
   public static void insertion(Comparable[] a, int lo, int hi){
       for (int i = lo + 1; i <= hi; i++){
           for (int j = i ; j > lo && a[j-1].compareTo(a[j]) > 0 ; j--){
               exch(a,j-1,j);
           }
       }
   }

2. 归并时两个子数组，如果左半边的最大值小于右半边的最小值，那么不用归并

   private static void sort(Comparable[] a, int lo, int hi){
       if (hi <= lo) return;
       if ((hi - lo) < 4){
           insertion(a, lo, hi);
           return;
       }
       sort(a,lo,lo + (hi - lo)/2);
       sort(a,lo + (hi - lo)/2 + 1,hi);
       if (a[lo + (hi - lo)/2].compareTo(a[lo + (hi - lo)/2 + 1]) < 0) return;
       merge(a,lo,hi,lo + (hi - lo)/2);
   }

3. 为了节省将元素复制到辅助数组作用的时间，可以在递归调用的每个层次交换原始数组与辅助数组的角色。

下面代码是实现。实现的核心在于：

1) 每一层递归中，不论是使用插入排序，还是因为左半边右半边已经有序不需要归并，还是需要归并，都要保证dest的正确有序。
2) 进入下一层递归时，源数组和辅助数组角色交换。

public class Merge {

    public static void sort(Comparable[] a){
        Comparable[] aux = a.clone();
        //注意，要把a放在dest位置上，否则源数组会少一次归并操作
        sort(aux,a,0, a.length - 1);
    }

    private static void sort(Comparable[] src, Comparable[] dest, int lo, int hi){
        if (hi <= lo) return;
        if ((hi - lo) < 4){
          //注意，小数组的插入排序要在dest上进行
            insertion(dest, lo, hi);
            return;
        }
        //在进行下一层归并时，交换源数组和辅助数组，避免复制操作
        sort(dest,src,lo,lo + (hi - lo)/2);
        sort(dest,src,lo + (hi - lo)/2 + 1,hi);
        if (src[lo + (hi - lo)/2].compareTo(src[lo + (hi - lo)/2 + 1]) < 0) {
          //如果从源数组判断此次不需要归并，那么也将相应位置元素copy到dest，即保证dest的元素正确有序
            System.arraycopy(src,lo,dest,lo,hi - lo + 1);
            return;
        }
        //归并排序时保证dest的正确有序，这样在返回上一层归并时，这里的dest可以作为上一层的辅助数组
        merge(src,dest,lo,hi,lo + (hi - lo)/2);
    }

    private static void merge(Comparable[] src, Comparable[] dest, int lo, int hi, int mid){
        int i = lo;
        int j = mid + 1;
        for (int k = lo; k <= hi; k++){
            if (j > hi) dest[k] = src[i++];
            else if (i > mid) dest[k] = src[j++];
            else if (src[i].compareTo(src[j])>=0) dest[k] = src[j++];
            else if (src[i].compareTo(src[j])<0) dest[k] = src[i++];
        }
    }

    public static void insertion(Comparable[] a, int lo, int hi){
        for (int i = lo + 1; i <= hi; i++){
            for (int j = i ; j > lo && a[j-1].compareTo(a[j]) > 0 ; j--){
                exch(a,j-1,j);
            }
        }
    }
}

上面的是自顶而下的归并，还有自底向上的归并。递归实现的归并排序是算法设计中分治思想的典型应用，即将一个大问题分解成小问题分别解决，再用小问题的答案来解决大问题。在自顶而下的递归中就是这样，在每一次递归中，都降低了数组长度，最后用最深处的微型数组归并结果，反过来求上层递归的答案。
其实，由于我们知道上层递归是如何使用下层递归的结果的，所以这里的归并排序可以不使用递归，利用循环，自底向上，先将卫星数组归并，比如先归并长度为1的数组，再归并长度为2的长度为4的，这样下去，将整个数组归并。这样的代码量更少。

public static void sort(Comparable[] a){
    aux = new Comparable[a.length];
    int N = a.length;
    for (int sz = 1; sz < N; sz *= 2){
        for (int lo = 0; lo < N - sz; lo = lo+sz*2){
            int hi = min(lo+sz*2-1,N-1);
            merge(a,lo,hi,lo + (hi-lo)/2);
        }
    }
}

基于比较的排序算法

我们讨论的都是基于比较的排序算法，这些算法的复杂度有上限。
命题：没有任何基于比较的算法能够保证使用少于lg(N!)~NlgN次比较将长度为N的数组排序。
证明：首先假设没有重复的主键，因为任何排序算法都应该能够处理这种情况。使用二叉树表示所有的比较。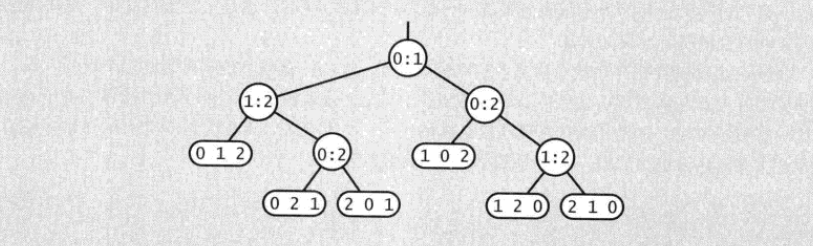

上图是N=3的比较树，叶子节点表示排序完成，内部节点表示a[i]和a[j]的一次比较操作，左子树表示a[i]小于a[j]时进行的其他比较，右子树表示a[i]大于a[j]时的其他比较。从根节点到叶子节点的所有路径表示在实际排序中，可能遇到的所有比较。
比较树中至少应该有N!个叶子节点，因为长度为N的数组，共有N!中排列方式，如果某个比较树的叶子节点小于N!,那么肯定有一些排列顺序被遗漏，基于这个比较树的算法在使用时，对于某些输入就无法正确的排序。
在排序算法中，我们通常关心比较的次数，而最多比较次数就是比较树的高度。高为h的二叉树最多叶子节点$2^h$，比较树中的叶子节点（就是所有的比较路径）数量N!,那么就有$N!<2^h$, 即$h="">\log{N!}$
上面的式子告诉我们在设计排序算法时所能达到的最佳效果。即比较次数最低是NlgN。

快速排序

归并排序虽然将算法时间复杂度降低到NlogN，但是需要一个与N成正比的辅助栈，而快排则避免了这个缺点，快排是原地排序，只需要一个很小的辅助栈。
快排的优点：

1. 时间复杂度为NlogN
2. 原地排序，只需要一个很小的辅助栈
3. 内循环比大多数排序都要小
4. 归并和希尔排序比快排慢，原因就是他们在内循环中还有移动复制操作。
   缺点：
5. 脆弱，在实现时要非常小心才能避免低劣的性能，许多错误都能导致快排的性能只有平方级别。比如在切分不平衡时可能导致快排极为低效，例如第一次从最小元素切分，第二次从第二小元素切分，这样每次只能移动一个元素，导致一个大数组需要切分很多次，事实上，这种极端情况下会比较$$\frac{1}{2}N^2$$次，我们可以在快排前将数组打乱以避免这种情况。
6. 快排效率依赖切分数组的效果，最好的情况是每次都能将数组对半分。

   public class Quick {
       public static void sort(Comparable[] a){
           sort(a,0,a.length-1);
       }
   
       private static void sort(Comparable[] a, int lo, int hi){
           if (lo>=hi) return;
           int j = partition(a,lo,hi);
           sort(a,lo,j-1);
           sort(a,j+1,hi);
       }
   
       private static int partition(Comparable[] a, int lo, int hi){
           Comparable tmp = a[lo];
           //因为lo位置的元素作为切分元素，所以这里本可以设置为lo+1，之所以设置为lo，是为了后面的先++lo做准备
           int lf = lo;
           //同理这里设置为hi+1，是为后面先--ri做准备
           int ri = hi + 1;
           while(true){
             //先判断界限，避免溢出，不停循环至第一个大于切分元素的位置
               while (++lf <= hi && tmp.compareTo(a[lf]) > 0);
               while (--ri >= lf && tmp.compareTo(a[ri]) < 0);
               if (lf>=ri) break;
               exch(a,lf,ri);
           }
           exch(a,lo,ri);
           return ri;
       }

算法改进

1. 切换到插入排序，在微型数组长度较短的情况下，使用插入排序比继续递归要快，一般长度在5-15之间(大多数基于递归的排序都可以这样做)。

private static void sort(Comparable[] a, int lo, int hi){
    if (hi > lo + 10) insertion(a,lo,hi);
    if (lo>=hi) return;
    int j = partition(a,lo,hi);
    sort(a,lo,j-1);
    sort(a,j+1,hi);
}
private static void insertion(Comparable[] a, int lo, int hi){
    for (int i = lo; i <= hi; i++){
        for (int j = i; j > lo && a[j].compareTo(a[i]) > 0; j--){
            exch(a,i,j);
        }
    }
}

1. 三取样切分，使用子数组中一小部分元素的中位数来切分，人们发现将取样大小设为3并用大小居中的元素切分效果最好。还可以将切分元素放在数组末尾作为哨兵来去掉数组边界检查。

   private static int partition(Comparable[] a, int lo, int hi){
       int x = median(a,lo,lo+1>a.length-1?a.length-1:lo+1,lo+2>a.length-1?a.length-1:lo+2);
       Comparable tmp = a[x];
       exch(a,x,lo);
       int lf = lo;
       int ri = hi + 1;
       while(true){
           while (++lf <= hi && tmp.compareTo(a[lf])>0);
           while (--ri >= lf && tmp.compareTo(a[ri]) < 0);
           if (lf>=ri) break;
           exch(a,lf,ri);
       }
       exch(a,lo,ri);
       return ri;
   }
   
   private static int median(Comparable[] x, int a, int b, int c){
       return x[a].compareTo(x[b])>0 ?
               (x[a].compareTo(x[c])>0 ? (x[b].compareTo(x[c]) > 0 ? b : c):a) :
               (x[a].compareTo(x[c])>0 ? a : (x[b].compareTo(x[c]) > 0 ? c : b));
   }

2. 三项切分快速排序

对于包含大量重复元素的数组，使用三项切分将排序时间从线性对数降低到线性级别。性能优于普通快排

public static void sort3Ways(Comparable[] a, int lo, int hi){
    if (lo>=hi) return;
    Comparable tmp = a[lo];
    int i = lo+1;
    //始终等于tmp的最左位置
    int lt = lo;
    //一次循环结束后，gt刚好在等于tmp的最右位置
    int gt = hi;
    while(i<=gt){
        int m = tmp.compareTo(a[i]);
        if (m>0) exch(a,i++,lt++);
        //这里的i没有+1，是因为从右边换过来的item大小未知，需要在进行一次比较
        else if (m<0) exch(a,i,gt--);
        else i++;
    }
    sort3Ways(a,lo,lt-1);
    sort3Ways(a,gt+1,hi);
}

private static void exch(Comparable[] source,int i, int j){
    Comparable tmp = source[j];
    source[j] = source[i];
    source[i] = tmp;
}

优先队列

队列中的元素有优先级，最大有限队列，最小优先队列。以最大优先队列为例，这样的数据结构要求支持两种操作，删除最大元素和插入元素，这里我们学习基于二叉堆数据结构的一种优先队列的经典实现方式，用数组保存元素并按照一定条件排序，以高效的实现删除最大元素和插入元素操作。
插入一列元素后一个一个的删除最小元素，就可以完成排序，堆排序算法就是源于优先队列的实现

实现

数组实现（无序）

参考下压栈的实现，插入时直接将元素插入到数组内，删除最大值时使用一个内循环获得最大元素，然后将最大元素与边界元素互换并删除最大元素。

数组实现（有序）

插入时将所有较大元素向右移动一格保持数组有序，这样最大元素始终在边界

链表表示

与数组实现类似，要么插入耗时删除高效，要么插入高效删除耗时

使用无序实现是惰性方法，我们仅在需要的时候才找出最大元素，使用有序实现是积极方法，在插入时保证有序。对于简单的队列和栈，所有操作都可以在常数时间内完成，而优先队列的最坏情况会达到线性时间。而基于数据结构堆的实现能保证插入和删除操作都能更快的执行。

二叉堆

数据结构二叉堆的定义：当一个二叉树的每个节点都大于等于他的两个子节点，它被称为堆有序，就是二叉堆。
根节点最大

数组实现二叉堆

位置k的节点的父节点的位置是
$\biggl\lfloor\frac{k}2\biggr\rfloor$，而他的两个子节点分别是2k和2k+1。这样在数组中使用索引在树中移动，很方便。根节点在数组索引为1的位置（不使用第一个位置）。

public class MaxPQ {
    private Comparable[] pq;
    private int N = 0;
    public MaxPQ(int maxN){
        pq = new Comparable[maxN + 1];
    }

    //插入操作，先插入到二叉堆最后位置，再上浮，保证堆有序
    public void insert(Comparable a){
        pq[++N] = a;
        swim(N);
    }

    //当元素比父节点大时，上浮保证堆有序
    private void swim(int k){
        while(k>1 && pq[k].compareTo(pq[k/2]) > 0){
            exch(k,k/2);
            k = k/2;
        }
    }
    //当元素比子节点小时，下潜保证堆有序
    private void sink(int k){
        while (2*k<=N){
            int j = 2*k;
            if (j<N && pq[j].compareTo(pq[j+1]) < 0) j++;
            //如果父节点不比子节点小，结束循环
            if (pq[k].compareTo(pq[j])>0) break;
            exch(k,j);
            k = j;
        }
    }

    //删除最大节点分两步，现将最后的节点与首节点交换，再下潜首节点
    public Comparable delMax(){
        Comparable max = pq[1];
        exch(1,N--);
        pq[N+1] = null;
        sink(1);
        return max;
    }

    private void exch(int a, int b){
        Comparable tmp = pq[a];
        pq[a] = pq[b];
        pq[b] = tmp;
    }
}

对于一个含有N个元素的基于堆的优先队列，插入操作只需不超过lgN+1次比较，删除最大元素需要不超过2lgN次比较。

优化二叉堆

1. 调整数组大小
2. 索引优先队列，暂不研究

堆排序

我们可以把任意优先队列变成一种排序方法：将所有元素插入一个最小优先队列，再重复删除最小元素即可。我们基于堆实现一种排序方法。

基于堆的排序

1. 用数组实现堆，首先将所有元素直接插入数组中
2. 将前半部分元素倒序做下潜操作
3. 从最后一个元素开始逐个做下潜操作

   public void sort(Comparable[] a){
       //N是有效元素大小（除去首位）
       int N = a.length-1;
       for (int i = N/2; i >= 1; i--){
           sink(a,i,N);
       }
       //将首位与最后一个交换，交换后，N减1（这是因为交换后最大元素已经在最后了，之后的操作与最后的最大元素无关），再做sink操作，
       while(N>1){
           exch(a,N--,1);
           sink(a,1,N);
       }
   }
   
   private void exch(Comparable[] pq,int a, int b){
       Comparable tmp = pq[a];
       pq[a] = pq[b];
       pq[b] = tmp;
   }
   
   private void sink(Comparable[] pq,int k,int N){
       while (2*k<=N){
           int j = 2*k;
           if (j<N && pq[j].compareTo(pq[j+1]) < 0) j++;
           if (pq[k].compareTo(pq[j])>0) break;
           exch(pq,k,j);
           k = j;
       }
   }

堆排序优化

先下沉再上浮：在下沉过程中可以将较大的元素直接放入堆底，再将其上浮，这样可以减少比较次数。
堆排序是目前已知的唯一能够同时最优利用空间和时间的方法。在最坏的情况下也能保证2NlgN次比较和恒定的额外空间。

各算法对比