算法 | 大巧不工

1 开平方

求常数a的开平方，其实就是对于函数$f(x) = x^2 -a$求解$f(x) = 0$的$x$。这个函数在$x>0$时单调递增，可以使用牛顿法逐步逼近。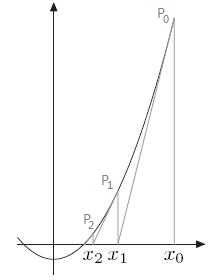

如图所示，先取一个值$x_0$,假设$x_0$是解，判断$x_0$不是解之后，使用$x_0$点的倒数求$x_1$，以此方式逐渐逼近正解。示例代码如下：

static double sqrt(double s){
  //当所求解与小于该值时，认为已求得正解
    double err = 1E-15;
    double t = s;
    while(Math.abs(t - s/t) > err){
        t = (t + s/t)/2;
    }
    return t;
}

2 float的表示方法

java中flaot采用IEEE 754标准，四字节32位0-31，分为三部分，符号位，指数位，尾数位。
|符号位 | 指数位 | 尾数位 |
|——-|——-|——-|
| 1bit | 8 bit | 23 bit|
(1).符号位(S)：最高位（31位）为符号位，表示整个浮点数的正负，0为正，1为负；
(2).指数位(E)：23-30位共8位为指数位。根据IEEE754说明，指数的底数可能为2或者10(java中使用2)，规定指数位减去127为指数，取值范围：-127~128，表达式为：$2^{E−127}$。另外，标准中，还规定了，当指数位8位全0或全1的时候，浮点数为非正规形式（这个时候尾数不一样了），所以指数位真正范围为：-126~127。
(3).尾数位(M)：0-22位共23位为尾数位，表示小数部分的尾数，即形式为1.M或0.M，至于什么时候是1，什么时候是0，则由指数和尾数共同决定。小数部分最高有效位是1的数被称为正规（规格化）形式。小数部分最高有效位是0的数被称为非正规（非规格化）形式，其他情况是特殊值。最终float的值 = $(-1)^{S} \cdot 2^{E-127} \cdot (1.M)$。
所以java中的float这样表示，以8.25为例：
首先将8.25转换为二进制1000.01，注意转换过程中整数部分与小数部分的区别，表示称二进制的科学计数法为$1.0001\cdot2^3$，也就是说,任何一个数都的科学计数法表示都为$1.xxxx\cdot2^3$，因为任何情况下，首位必为1，所以就省略首位1，将xxxx作为尾数位，所以虽然尾数位是23位，其实表示的是24位。然后指数3+127=130，把130转换成二进制保存在指数位。符号位为1。所以8.25在内存中的表达就是：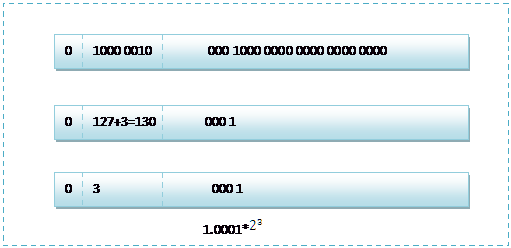

这样就能解释float的精度问题了，float的有效位数由尾数位决定，23位尾数加上省略的尾数位最高位1，共24位，$2^24 = 16777216$，也就是说最高有效位数8位，但是16777216并不能覆盖所有8位数，所有最高有效位数是7位。另外，由于在计算过程中会出现四舍五入的情况，所以，在float中，前六位是绝对精确地，第七位可能不精确。
总结，float有效位数7位，精确度6位。

3 判断素数

原理：合数的最小质因子一定小于等于它的平方根。

static boolean isPrime(int n){
    if (n < 2) return false;
    for (int i = 2; i * i <= n; i++){
        if (n%i == 0) return false;
    }
    return true;
}

4 调和数列与调和级数

调和数列是自然数的倒数构成的数列，其前n项和就是调和级数。求调和级数直接便利求和

5 补码计算原理

在计算机中，所有的数都是按照补码来存储并计算的，那么什么是补码呢？要完美的理解补码，就要完全抛开课本上以及博客上的关于原码高位不变低位取反加一的论调，并不是说他们是错的，只是取反加一以及最高位作为符号位的说法更适合计算方便，事实上计算机的计算方式确实是高位不变低位取反加一，但这种理解并不准确，相反完全增加了理解补码计算的难度。那么如何理解补码呢？
首先，要理解模。以钟表为例，假如现在是三点，如果要求将时间回退五个小时，你会怎么办？两种方法：

顺时针拨动时针7格
逆时针拨动时针5格

第二个方法理解起来非常简单，回退嘛，那就逆时针，这里要着重说的是第一种，为什么顺时针也能达到逆时针的效果呢？其实，顺时针拨动7格，就是拨动(12-5)格，这里的12就是模，模的存在，将处于模之内的数构成一个环，环内的数都可以通过正向增长或逆向增长的方式变为环内的另一个数(其实就是取膜运算%)。若数超过模，那么就做取模处理，所以值永远小于模。如果时钟的例子不明朗，那么以十进制为例，以10为模，那么，6加7是3，6减3也是3，这就是模10的“环”。
那么计算机中为什么要利用模来进行计算呢？
因为计算机中只有加法计算，没有减法，任何减法运算都必须转换为加上一个负数来进行。这就带来一个问题，怎么表示这个负数，并且保证计算结果正确呢？这个时候就要使用补码了。
现在知道，模有两个性质：

存在一个环，当数持续增长到溢出时，会回到最小值
模内的数无论做多少次加减，其值始终小于模，模类似一个极值

利用上述两个性质，我们可以将计算机的减法运算简化。
在模的范围内，两个相加等于的模得数互为补数，以模10为例，1和9，2和8都互为补数，那么，模范围内的减法$a-b$就可以变换为$a+b\text{的补数}$，还是以模10为例
$$5-1 = 5 + (10 -1) = 14 (1)$$
14溢出要取模，最终结果是4，计算正确。其实这个过程里的+10就相当于绕环一圈回到正确位置，并不影响计算结果，但也因为这一圈，消除了减法，转换成了加法计算。
那么，在计算机内是如何实现的呢？
计算机中实现时，牵扯到一个问题，那就是式1的(10-1)在内存中该如何表示，因为既然我们要使用$a+b\text{的补数}$的方式计算，那么$b\text{的补数}$必定要满足两个要求：

避开减法运算，不能像式1那样还存在减法
在二进制中能直接通过位运算得到补数

于是，大牛们想到了一个完美的办法，映射。
我们知道，长度为n的二进制数范围是$\left[0,2^n-1\right]$(后面成为集合Z)，共$2^n$个数,模为$2^n$。现在我们要表示$\left[-2^{n-1},2^{n-1}-1\right]$这个范围的数，也就是要把$\left[-2^{n-1},2^{n-1}-1\right]$内所有的数刚好映射到$\left[0,2^n-1\right]$上。主要分两部分：

对于在$\left[0,2^{n-1}-1\right]$范围内的数，可以保持原样(这个对应求补码的正数不变)
对于在$\left[-2^{n-1},0\right)$的数，使用补数映射到Z上，即对于x，在Z上有$2^n-\left|x\right|$与之对应，也就是说负数用她的绝对值的补数来表达。这也解释了为什么$-2^{n-1}$可以使用$1000 0000 …$这样的二进制来表达，因为刚好映射上了啊！这个映射过程其实刚好对应求负数补码的过程：符号位不变并取反加一，但是事实上，在补码的计算中，并不存在符号位。

那么，实际计算中，补码如何起作用呢？在上面的十进制例子中，式1，5-1的计算变换为5 + (10 -1)，加10相当于绕环一圈，计算结果14溢出取模后结果是4。也就是说，使用补数进行计算，只要真实结果没有溢出，那么可以直接拿补数相加的结果作为真实结果。
回到二进制，在任意的二进制加减法中，因为使用了上述原理(就是补码)计算，所以补码的计算结果可以直接作为正确结果。需要注意的是，不同于上述十进制的例子，在计算机中，如果补码计算结果在$\left[0,2^{n-1}-1\right]$内，那么，所得结果即为正确答案，如果补码计算结果在$\left[-2^{n-1},0\right)$内，那么，所得结果需要做一个反向映射才是正确答案，但是内存中存储的始终是未做反向映射的那个值。举例来说：
在8位计算机中，要把$\left[-128,127\right]$映射到$\left[0,255\right]$上，那么30-100其实就是30+(256-100) = 186,注意内存中始终存储的是186，但是当我们要读出来这个数时，cpu做了反映射 256-186 = 70，70就是所求的正确答案。

tip：其实映射的过程就是一个函数，函数图像为：

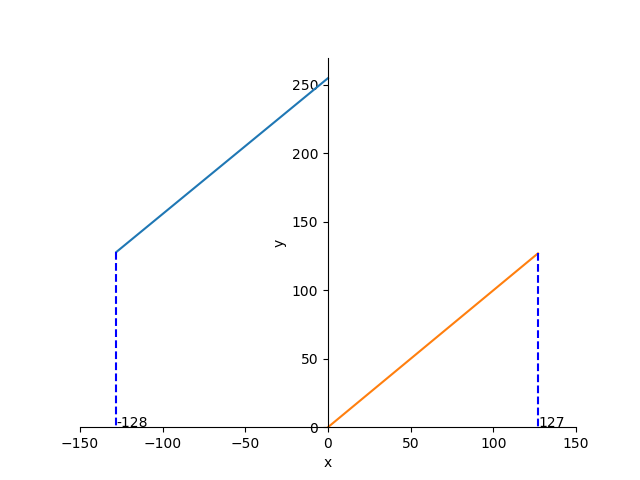
函数值为补码，x为真实值，内存中按照补码存储，需要真实值时做反映射。

所谓的符号位与取反加一

我们知道，书本中说到补码的时候，都会从遵从原码反码补码的顺序，好像这三者是有着递进关系的，实际上并不是这样。但是我们所说的映射过程和由原码求补码是有一定关联的，下面以8位二进制为例作出解释。
首先8位二进制在内存中共有0000 0000到1111 1111共256中情况，可以表示[-128,127]的范围，根据上述的映射原理，这个范围要分两个部分对待[-128,0)和[0,127]：
对于数字2，2位于上图右半部分，补码映射函数是$f(x) = x$，其实这个函数映射关系就对应了书本上的正数的补码不变，所以补码是0000 0010,注意这个过程中并没有通过原码=>补码来转换，而是直接用了映射，刚好对应。
对于数字-2，-2位于上图左半部分，补码映射函数$f(x) = 256 - \left|x\right|$，具体计算是什么样呢？

1 0000 0000 - 0000 0010
= 1111 1111 + 0000 0001 - 0000 0010
= (1111 1111 - 0000 0010) + 0000 0001
= (1000 0000 + 0111 1111 - 0000 0000 - 0000 0010) + 0000 0001
//第一个括号表示高位不变，第二个括号表示低位取反，最后加一
= (1000 0000 - 0000 0000) + (0111 1111 - 0000 0010) + 0000 0001

这说明所谓的取反加一并没有什么神秘，只是二进制中求补数的一种便捷的分配算法而已。

关于反码

我们知道，书本中说到补码的时候会从反码讲解过来，好像补码由反码加一而来，其实这么理解并不合适。上面已经说过补码的映射原理，其实求反码也是一个映射过程。还是以8位二进制为例，求反码的过程其实就是求原数字关于255的补数(对应到补码的模来理解，只不过这里的模是255)。

对于-2，反码计算

1111 1111 - 0000 0010
= 1111 1111 - 0000 0010
= (1000 0000 + 0111 1111 - 0000 0000 - 0000 0010)
//第一个括号表示高位不变，第二个括号表示低位取反，同样取反的言论只是一个计算而已，真正起作用的是求补数
= (1000 0000 - 0000 0000) + (0111 1111 - 0000 0010)

那么求反码的过程还是把[-127,127]映射到[0,255]上。但是8位是可以表示256个数的，而模为255的时候只能表示255个数。多出一个怎么办？我们观察到，[-127,-1]会映射到[128，254]上，那反码255，也就是1111 1111表示什么呢？实际上，1111 1111在加一就是0000 0000，在反码计算中，这两个都可能代表0，一个是所谓的+0，一个是所谓的-0。也就是说，相比于补码，由于反码的模范围比它要表达的数范围大1，模的环出现了”裂缝”，被两个0打断，这也是计算机中补码优于反码计算的原因。

以2-2为例，解释两个0的现象

2-2
= 0000 0010 + 1111 1111 - 0000 0010
= 0000 0010 + 1111 1101
= 1111 1111

5 int溢出

根据补码的映射与模环的理解，对于int的溢出后的值，可以这样求，int最大值2147483647：

比如2147483648，位于图像左半边，根据映射关系2147483648表示
(2147483648 - 4294967296) = -2147483648

比如2147483649，位于图像左半边，根据映射关系2147483649表示
(2147483649 - 4294967296) = -2147483647

比如4294967297，先取模4294967297%4294967296为1，位于图像右半边，根据映射关系4294967297表示1

关于int溢出例子

Math.abs(-2147483648) = 2147483648，2147483648溢出，根据环，最后结果为-2147483648

6 String的intern()

7 1/0与1.0/0.0

前者是devide by zero异常，后者是无限大。
1/0出现异常的原因是，1除以0在计算机中无法计算，除法过程会无限持续，另外，即使默认1/0结果是无限大或者NAN也不行，因为在int中没有定义正无穷负无穷和nan，整数是有限的。
1.0/0.0结果是无穷大，这是因为float中的0并不完全是0，根据float在内存中的表达方式，0.0是极其接近0的一个小值，所以首先这个除法过程是可以进行的。另外在float中也定义了正负无穷，所以有结果。

8 float的三个值

正无穷，负无穷，NaN。
1.0/0.0 = POSITIVE_INFINITY(正无穷),It is equal to the value returned by Float.intBitsToFloat(0x7f800000).
-1.0/0.0 = NEGATIVE_INFINITY(负无穷),It is equal to the value returned by Float.intBitsToFloat(0xff800000).
0.0/0.0 = NaN
POSITIVE_INFINITY - POSITIVE_INFINITY = NaN
另外需要注意的是，Float的MAX_VALUE和MIN_VALUE表示的是float所能表示的最大正数和最小正数(不是最小的负数)

double也有相似的三个值。

9 负整数除法和模

-14/3 = -4 余 -2
14/-3 = -4 余 2
-14/-3 = 4 余 -2
遵循向零取整：什么意思呢？比如两个正数10和4相除，商2.5，向零取整为2，那么余10-42 = 2；
同理，在负数加入进来后，也遵循向零取整，如 -14/3，商-4.67，向零取整-4，那么余-14-(-43) = -2;再如14/-3商-4.67，向零取整-4，余14-(-3 * -4) = 2;

负数的模与上面同理。

10 位运算符

& | ^

11 求整数的二进制字符串

public static String getBanaryString(int n){
  String result = "";
  for(int i = n; i >= 1 ; i /= 2){
    result = i%2 + result;
  }
  return result;
}

12 递归计算ln(N!)

这个比较简单

public static double calLn(int n){
    if(n == 1){
      return 0;
    }
    return calLn(n-1) + Math.log(n);
}

13 递归计算二项分布

算法4中的程序

public static double bino(int n, int k, double p){
  if(n == 0 && k == 0){
    return 1;
  }
  if(n < 0 || k < 0){
    return 0;
  }
  return p*bino(n-1,k-1,p) + (1-p)*bino(n-1,k,p);
}

在出口出增加$n

public static double bino(int n, int k, double p){
  if(n == 0 && k == 0){
    return 1;
  }
  if(n < 0 || k < 0 || n < k){
    return 0;
  }
  return p*bino(n-1,k-1,p) + (1-p)*bino(n-1,k,p);
}

但是上面的程序递归深度还是很高，k值到50左右就很难算出来了，只能用空间还换取时间，使用数组缓存已经计算出来的结果，程序如下：

public static double[][] M;
public static double bino(int n, int k, double p){
  num++;
  if(n == 0 && k == 0){
    return 1;
  }
  if(n < 0 || k < 0 || n < k){
    return 0;
  }
  if(M[n][k] == -1){
    M[n][k] =  p*bino(n-1,k-1,p) + (1-p)*bino(n-1,k,p);
  }
  return M[n][k];
}
public static void main(String[] args) {
  int n = 100, k = 50;
  double p = 0.5;
  M = new double[n+1][k+1];
  for(int i = 0; i < n+1; i++){
    for(int j = 0; j < k+1; j++){
      M[i][j] = -1;
    }
  }
  System.out.print("bino " + bino(n,k,p)  + " num = " + num + "\n");
}

计算速度足够快，n = 100, k = 50，递归5201次。

使用循环实现

1	使用循环就是直接使用二项分布的公式了，代码没意思，不写了

14 求最大公约数

辗转相除法
原理：两个正整数a和b（a>b），它们的最大公约数等于a除以b的余数c和b之间的最大公约数。证明也很简单：
假设a,b最大公约数为t，则有a=mt,b=nt,a/b=c…r,那么，a=cb+r => r=a-cb,可以看出a-cb是a，b的线性组合，肯定能被t整除，而最大公约数肯定是小于余数的，所以就有上面的原理了。

//循环
public static int gcd(int m, int n){
    int r = 0;
    while(true){
      if ((r = m%n) == 0) {
        return n;
      }
      m = n;
      n = r;
    }
}
//递归
public static int gcd1(int m, int n){
  if (m%n == 0) {
    return n;
  }
  return gcd1(n,m%n);
}

相减法
原理：两个正整数a和b（a>b），它们的最大公约数等于a-b的差值c和较小数b的最大公约数。证明略。

public static int gcd2(int m, int n){
  int t = 0;
  while(m != n){
    if (m>n) {
      m = m-n;
    }else{
      n = n-m;
    }
  }
  return n;
}

辗转相除法的模运算在数字很大的时候效率不高，相减法在两个数相差很大的时候效率不高。
改进一下相减法并使用位运算可以提高效率：

当a和b均为偶数，$gcb(a,b) = 2gcb(a/2, b/2) = 2gcb(a>>1, b>>1)$
当a为偶数，b为奇数，$gcb(a,b) = gcb(a/2, b) = gcb(a>>1, b)$
当a为奇数，b为偶数，$gcb(a,b) = gcb(a, b/2) = gcb(a, b>>1)$

public static int gcd3(int m, int n){
  if (m == n) {
    return m;
  }
  if (m<n) {
    return gcd3(n,m);
  }
  if ((m&1) != 1 && (n&1) != 1) {
    return 2*gcd3(m>>1,n>>1);
  }else if ((m&1) != 1 && (n&1) == 1) {
    return gcd3(m>>1, n);
  }else if ((m&1) == 1 && (n&1) != 1) {
    return gcd3(m,n>>1);
  }else{
    return gcd3(n,m-n);
  }
}

15 最小公倍数

a，b最大公约数c，则最小公倍数时ab/c

16 求两个数互质

就是求两个数的最大公约数是否为1，为1则互质。互质的两个数还有一些其他的性质。可以使用这些性质优化算法，避免每次都求最大公约数。

两个不同的质数一定是互质数。
例如，2与7、13与19。
一个质数，另一个不为它的倍数，这两个数为互质数。
例如，3与10、5与 26。
1不是质数也不是合数，它和任何一个自然数（1本身除外）在一起都是互质数。如1和9908。
相邻的两个自然数是互质数。如 15与 16。
相邻的两个奇数是互质数。如 49与 51。
较大数是质数的两个数是互质数。如97与88。
两个数都是合数（二数差又较大），较小数所有的质因数，都不是较大数的约数，这两个数是互质数。
如357与715，357=3×7×17，而3、7和17都不是715的约数，这两个数为互质数。
两个数都是合数（二数差较小），这两个数的差的所有质因数都不是较小数的约数，这两个数是互质数。如85和78。85－78=7，7不是78的约数，这两个数是互质数。
两个数都是合数，较大数除以较小数的余数（不为“0”且大于“ 1”）的所有质因数，都不是较小数的约数，这两个数是互质数。如 462与 221
17 左移，右移，无符号右移
左移永远补0，所以无所谓左右。
需要注意的是，以补码保存的负数，在进行有符号移位操作后，仍能正确表示移位操作之后的负数。