锐化
锐化(image sharpening)是补偿图像的轮廓,增强图像的边缘及灰度跳变的部分,使图像变得清晰。从频域的角度理解是增强图像的高频分量。目前主流软件锐化方式主要有全局锐化和局部锐化,本文主要涉及全局锐化,局部今后另说。
全局锐化
原理:理论上来说,全局锐化是滤波算法的逆应用
滤波结果 = 过滤掉图像细节的输入图像
图像细节 = 输入图像 - 滤波结果
锐化结果 = 输入图像 + 锐化系数 X 图像细节
所以说有多少种滤波算法,就有多少中锐化算法。
锐化的核心目的是强化图像轮廓,比如人体的眼眶,帽子的帽沿,将非轮廓的地方锐化,对于增强整体的形态并无太大帮助。而全局锐化是将整个图像进行无差别增强,这也是全局锐化的不足之处。
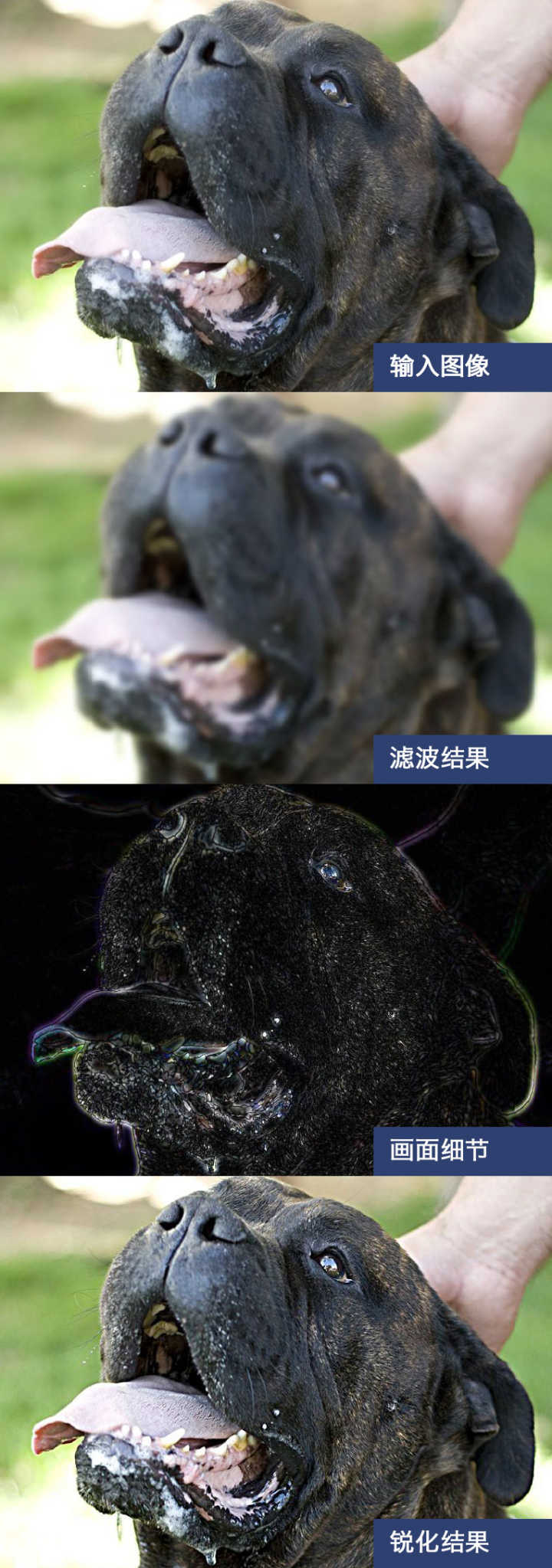
实际应用中,简单的全局锐化可以使用Unsharp Mask(USM)算法。
$$y(n,m) = x(n,m) + \lambda\,z(n,m)$$
其中,$x(n,m)$ 为输入图像,$y(n,m)$ 为输出图像,而$z(n,m)$ 为校正信号,在锐化中就是图像细节信号,一般是通过对$x$进行滤波获取。$λ$是用于控制增强效果的的一个缩放因子。
在传统的USM算法中,$z(n,m)$ 一般可以通过下式获取:
$$z(n,m)=4x(n,m)-x(n-1,m) -x(n +1,m)-x(n, m-1) -x(n,m+1)$$
图像滤波的过程就是卷积核对图像上所有像素点及其临近像素进行对应相乘叠加的结果。如图: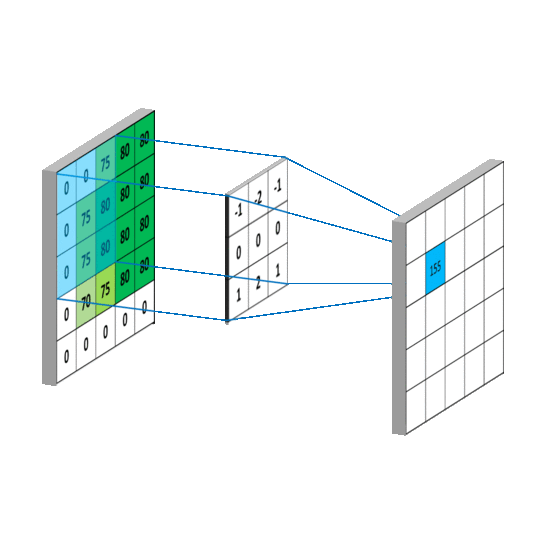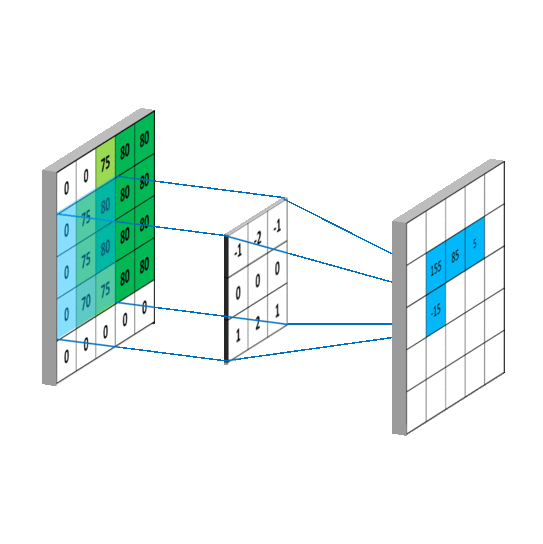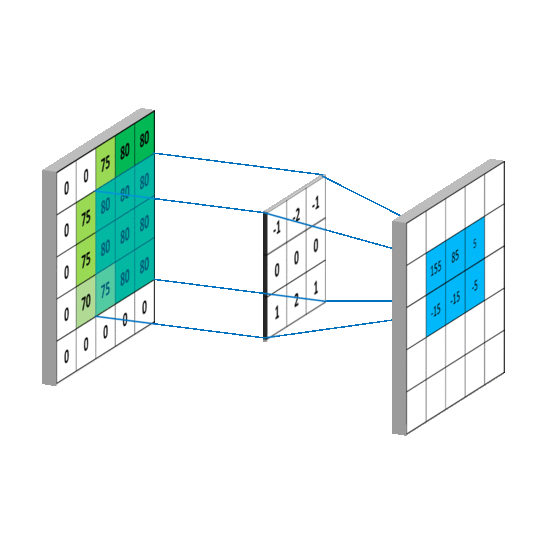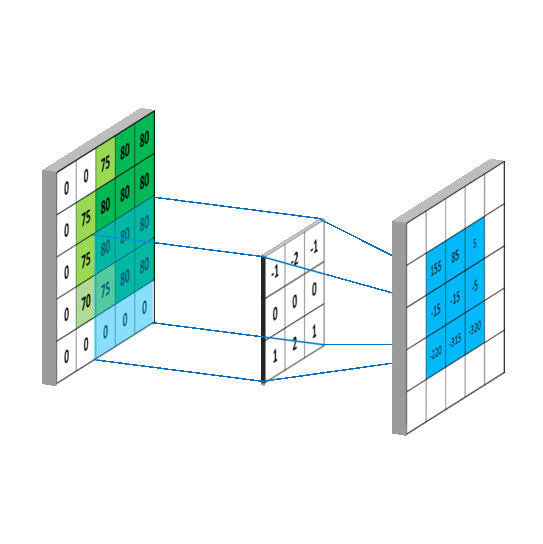
注意:这个对应元素相乘累加的过程,就是两个矩阵离散卷积的过程。
根据卷积定理:函数卷积的傅立叶变换是函数傅立叶变换的乘积,那么我们只要使矩阵B的频谱中不包含频率 $\omega$,就能保证卷积结果中也不包含频率 $\omega$,这就是滤波的由来。
上式对应的卷积核为
局部锐化
局部锐化可以弥补全局锐化的不足,将锐化的重心放在图像的边缘处(比如头发丝,脸颊),突出形体和轮廓。
这就需要做出边缘检测,目前流行算法
Laplician of Gaussian(LoG),据说PS中用于Edge Dectection的高反差保留以及照片边插画的核心算法都是这个。
滤波算法
根据卷积定理:函数卷积的傅立叶变换等于两个函数傅立叶变换的乘积,那么如果用于卷积的卷积核损失了高频或者低频的部分,卷积后的图像频谱相应的也会损失对应的频率,这就是滤波器的工作原理。
线性滤波器(均值滤波)
线性滤波器的原始数据与滤波结果是一种算术运算,即用加减乘除等运算实现,如均值滤波器(模板内像素灰度值的平均值)、高斯滤波器(高斯加权平均值)等。由于线性滤波器是算术运算,有固定的模板,因此滤波器的转移函数是可以确定并且是唯一的(转移函数即模板的傅里叶变换)。
卷积可以说是图像处理最基本的操作,但却非常有用。这个操作有两个非常关键的特点:它们是线性的,而且具有平移不变性shift-invariant。平移不变性指我们在图像的每个位置都执行相同的操作。线性指这个操作是线性的,也就是我们用每个像素的邻域的线性组合来代替这个像素。这两个属性使得这个操作非常简单,因为线性操作是最简单的,然后在所有地方都做同样的操作就更简单了。
2D卷积需要4个嵌套循环4-double loop,所以它并不快,除非我们使用很小的卷积核。这里一般使用3x3或者5x5。而且,对于滤波器,也有一定的规则要求:
- 滤波器的大小应该是奇数,这样它才有一个中心,例如3x3,5x5或者7x7。有中心了,也有了半径的称呼,例如5x5大小的核的半径就是2。
- 滤波器矩阵所有的元素之和应该要等于1,这是为了保证滤波前后图像的亮度保持不变。当然了,这不是硬性要求了。
- 如果滤波器矩阵所有元素之和大于1,那么滤波后的图像就会比原图像更亮,反之,如果小于1,那么得到的图像就会变暗。如果和为0,图像不会变黑,但也会非常暗。
- 对于滤波后的结构,可能会出现负数或者大于255的数值。对这种情况,我们将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
平滑均值滤波器
$$\frac{1}{9}\left(\begin{matrix} 1 & 1 & 1\ 1 & 1 & 1 \ 1 & 1 & 1\end{matrix} \right)$$
这是一个低通滤波器,其频谱的高频部分幅值很低甚至为零,也就是说会过滤掉高频部分,结果是将图像进行平滑处理。锐化均值滤波器
$$\left(\begin{matrix} -1 & -1 & -1\ -1 & 8 & -1 \ -1 & -1 & -1\end{matrix} \right)$$
这是一个高通滤波器,其频谱的低频部分幅值很低甚至为零,也就是说会过滤掉低频部分,结果是将图像进行锐化处理。高斯滤波器
高斯滤波器是低通滤波,滤波后图像被平滑的程度取决于标准差。它的输出是领域像素的加权平均,同时离中心越近的像素权重越高。因此,相对于均值滤波(mean filter)它的平滑效果更柔和,而且边缘保留的也更好。
高斯滤波简单说就是卷积核的概率分布服从高斯分布。自然界里高斯分布遍布各处,使用高斯分布有一定的理由。
3X3高斯卷积核:
$$\frac{1}{16}\left(\begin{matrix} 1 & 2 & 1\ 2 & 4 & 2 \ 1 & 2 & 1\end{matrix} \right)$$
5X5高斯卷积核:
$$\frac{1}{273}\left(\begin{matrix} 1 & 4 & 7 & 4 & 1 \ 4 & 16 & 26 & 16 & 4 \ 7 & 26 & 41 & 26 & 7 \ 4 & 16 & 26 & 16 & 4 \ 1 & 4 & 7 & 4 & 1\\end{matrix} \right)$$非线性滤波器
非线性滤波器的原始数据与滤波结果是一种逻辑关系,即用逻辑运算实现,如最大值滤波器、最小值滤波器、中值滤波器等,是通过比较一定邻域内的灰度值大小来实现的,没有固定的模板,因而也就没有特定的转移函数(因为没有模板作傅里叶变换),另外,膨胀和腐蚀也是通过最大值、最小值滤波器实现的。
对比度
锐化与对比度的区别
锐化可以理解为增加局部差异,增加对比度可以理解为拉开整体差异