卷积
函数定义:设:$f(x)$, $g(x)$ 是R1上的两个可积函数,作积分
$${\int_{-\infty}^{\infty}}f(\tau)\ast\,g(x-\tau)\,\mathrm{d}\tau$$
可以证明,关于几乎所有的实数$x$,上述积分是存在的。这样,随着$x$的不同取值,这个积分就定义了一个新函数$h(x)$,称为函数$f$与$g$的卷积,记为$h(x)=(f\ast\,g)(x)$。
容易验证,$(f\ast\,g)(x)=\,(g\ast\,f)(x)$,并且 $(f\ast\,g)(x)$ 仍为可积函数。这就是说,把卷积代替乘法,$L1(R1)$空间是一个代数,甚至是巴拿赫代数。
离散表达:
$$y(n) = \sum_{i=-\infty}^{\infty}x(i)h(n-i) = x(n)\ast\,h(t)$$
理解
首先要明确,卷积只在线性时不变系统起作用,所以我们接下来的讨论均在此条件下进行。线性时不变系统:
- 线性系统:系统的输入和输出具有线性关系
- 时不变系统:系统的参数不随时间而变化,即不管输入信号作用的时间先后,输出信号响应的形状均相同,仅是从出现的时间不同,与系统状态无关。
物理意义:对于输入信号$f(τ)$,响应函数$g(τ)$,在t时刻的输出信号即为两者的卷积:
$${\int_{-\infty}^{\infty}}f(\tau)g(t-\tau)\,\mathrm{d}\tau$$
该式与上面公式区别仅在于改变了变量符号为时间t,主要为了便于理解。
离散情况
那么,为什么将两个时间信号这样积分,或者说求卷积就是t时刻的输出信号呢?举例来说:
第一年,小明存入100元钱,年利率是5%,按复利计算(即将每一年所获利息加入本金,以计算下一年的利息),那么在五年之后他能拿到的钱数是$100(1+5\%)^5$,如此类推,第二年存入100,四年后能拿到$100(1+5\%)^4$,连续存五年,列表如下:
| 本金 | 第一年 | 第二年 | 第三年 | 第四年 | 第五年 |
|---|---|---|---|---|---|
| $\small100$ | $\small100(1+5\%)^1$ | $\small100(1+5\%)^2$ | $\small100(1+5\%)^3$ | $\small100(1+5\%)^4$ | $\small100(1+5\%)^5$ |
| $\small100$ | $\small100(1+5\%)^1$ | $\small100(1+5\%)^2$ | $\small100(1+5\%)^3$ | $100(1+5\%)^4$ | |
| $\small100$ | $\small100(1+5\%)^1$ | $\small100(1+5\%)^2$ | $\small100(1+5\%)^3$ | ||
| $\small100$ | $\small100(1+5\%)^1$ | $\small100(1+5\%)^2$ | |||
| $\small100$ | $\small100(1+5\%)^1$ | ||||
| $\small100$ |
最终,在第五年小明拿到钱:
$$\small100(1+5\%)^1 + 100(1+5\%)^2 + 100(1+5\%)^3 + 100(1+5\%)^4 + 100(1+5\%)^5$$
对应到上面的离散公式:
$$\sum_{i=0}^{5}x(i)h(5-i)$$
其中,$x(i) = 100$,$h(5-i) = {(1+5)}^{5-i}$
这里计算结果即为在第五年拿到的总钱数,也是小明存钱函数(输入信号)$x(i) = 100$与复利计算函数(响应函数)$h(i) = {(1+5)}^{i}$ 的卷积结果。
连续情况
初次看到卷积积分公式时,对于将两个关于$x$的函数在$τ$上积分不理解,这也直接导致对卷积数学意义和物理意义的理解偏差。
举例,假如有响应函数$h(t)$,那么对于输入信号$f(t)$,在时刻T,将两者反褶相乘积分,画图举例 ()
其实,$τ$也是时间,只是我们在积分公式中,给定了时刻$t$。而给定t意味着输入信号与响应函数的相对位置确定,这就然后让$τ$在 $(-\infty,t]$ 上积分,我们知道积分可以看作无数个值的累加,那么从左往右的累加过程,就是 $(-\infty,t]$ 中所有时刻输入信号在响应函数作用下对t时刻输出信号的累加,这就是卷积。那么为什么会出现$τ$、$t-τ$、$τ+(t-τ)$刚好是t的看似巧妙的情况呢?这是因为,如果当前时间为t,那么在0时刻的输出信号在t时刻的响应函数就是$h(t-0)$,同样的,在τ时刻的输出信号在t时刻的响应函数就是$h(t-τ)$,没有什么数学上的巧合与美丽,只有实际的应用与计算。其实写到这里,已经觉得是在说废话了。
假设在一个线性时不变系统中,输入信号$x(t)$, 冲击信号$h(t)$,那么输出信号即为$x(t)\ast\,h(t)$,其步骤为:
- 变换变量$t$为$τ$
- 冲击信号反褶 $h(-τ)$
- 时移 $h(t-τ)$
- 相乘 $x(τ)h(t-τ)$
- 积分
这是卷积计算的步骤,很好理解,很好计算,这里权作记录。
矩阵卷积
矩阵的卷积与一维离散卷积类似,只是反转平移的过程变为将响应矩阵旋转180度,这样刚好形成$f(τ)h(t-τ)$。
比如,现有矩阵A,B:
$${A} = \left(\begin{matrix} 1 & 2 \ 3 & 4 \end{matrix} \right)\,\,\,\,\,\,{B} = \left(\begin{matrix} 5 & 6 \ 7 & 8 \end{matrix} \right)$$
变化矩阵B,三种方法:
- 直接旋转180
- 沿对角线分别反转
- 同时反转行和列
三种方法只是利用了矩阵基本性质,不赘述。
假设B翻转后得矩阵C:
$${C} = \left(\begin{matrix} 8 & 7 \ 6 & 5 \end{matrix} \right)$$
那么,AB卷积的过程就是是将AC矩阵对应位置的元素相乘,并将结果累加,在图像处理中经常用到这种方法。AB卷积结果为:
$$5\cdot8+6\cdot7+7\cdot6+8\cdot5 = 164$$
在深度学习中,矩阵卷积应用广泛,具体可参考 – 矩阵卷积
卷积定理
卷积定理是傅立叶变换满足的一个重要性质。卷积定理指出,函数卷积的傅立叶变换是函数傅立叶变换的乘积。具体分为时域卷积定理和频域卷积定理,时域卷积定理即时域内的卷积对应频域内的乘积;频域卷积定理即频域内的卷积对应时域内的乘积,两者具有对偶关系。
若
$$f_1(t)\leftrightarrow\,F_1(\omega)$$
$$f_2(t)\leftrightarrow\,F_2(\omega)$$
$F$ 表示傅里叶变换。
则时域卷积定理:
$$F(f_1(t)\ast\,f_2(t)) = F_1(\omega)F_2(\omega)$$
频域卷积定理:
$$F[f_1(t)f_2(t)] = \frac{1}{2\pi}F_1(\omega)F_2(\omega)$$
卷积定理揭示了时间域与频率域的对应关系。
去卷积
傅里叶
傅里叶级数
对于任意周期函数,都可以表示成一系列三角函数的和。
那么为什么可以做这种变换呢?这可以几何或者矩阵做类比,在三维空间几何中,我们可以用$(1,0,0),(0,1,0),(0,0,1)$三个空间向量的线性组合来表示这个空间中的所有向量,这三个向量两两正交,称为三维空间向量的基。同理从矩阵的角度看,单元矩阵的每行或者每列也是两两正交,那么每一行都可以看作这个矩阵空间的基,使用这些基向量的线性叠加可以表示任意一个矩阵,如下:
$$\left(\begin{matrix} 1 & 0 \ 0 & 1 \end{matrix} \right) = \left(\begin{matrix} 1 & 0 \ 0 & 0 \end{matrix} \right) + \left(\begin{matrix} 0 & 0 \ 0 & 1 \end{matrix} \right)$$
而对于函数,数学家也发现同样的现象,使用无数个相互正交的函数可以近似的表示任意一个周期函数,问题是这无数个两两正交的函数怎么找呢,三角函数刚好完美支持,而傅里叶级数选取的这个基函数就是三角函数,事实上,傅里叶级数可以有多种变化方式,三角函数只是其中一种。三角函数的正交性:
下面我们看傅里叶级数的表达,对于任意周期为T的函数,只要满足狄利赫里条件,则函数可以表达为:
$$f(x) = \sum_{k=1}^\infty(a_k\,sin(kx) + b_k\,cos(kx)) + \frac{a_0}{2}$$
其中:
$$a0 = \frac{2}{T}\int{-\frac{T}{2}}^{\frac{T}{2}}f(x)dx$$
$$ak = \frac{2}{T}\int{-\frac{T}{2}}^{\frac{T}{2}}f(x)sin(kx)dx$$
$$bk = \frac{2}{T}\int{-\frac{T}{2}}^{\frac{T}{2}}f(x)cos(kx)dx$$
关于$a_0$:将傅里叶级数两边在一个周期上同时积分,$sin$、$cos$的积分均为0,即可得$a_0$
关于$a_n$:等式两边同时乘以$sin(nx)$再进行积分,根据三角函数正交定理,只有同频率的元素在周期上的积分才不为零:
$$\int{-\frac{T}{2}}^{\frac{T}{2}}f(x)sin(kx)=\int{\frac{2}{T}}^2{a_n}\,sin(kx)^2dx$$
$$\int_{-\,\frac{T}{2}}^{\frac{T}{2}}f(x)sin(kx) = a_n\frac{T}{2}$$
即得$a_n$
同理得$b_n$
傅里叶展开后,原函数与展开式,以及展开式的频谱、相位关系图,现在有了各频率下的幅值和相位,原函数的频域信息就都体现出来了:
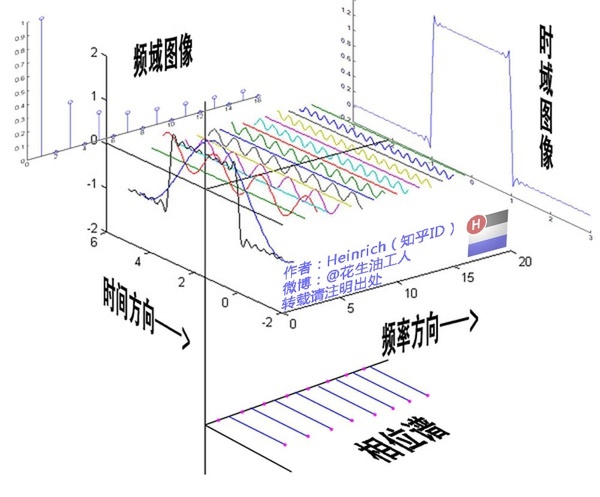
可以看出,将展开级数沿z轴放置,从图右边看,就是频谱,从上面看就是相位,需要注意的是,由于傅里叶级数中只使用了正弦和余弦函数,因此相位永远是0或者$\pi$,另外,级数展开后得频率非连续,是一个个独立的幅值,对应的频率是原函数频率的整数倍,这样的频谱是离散的。
下面的动图也有助于理解:
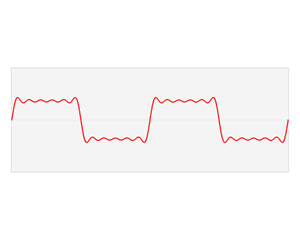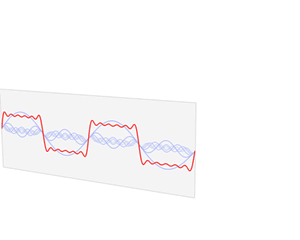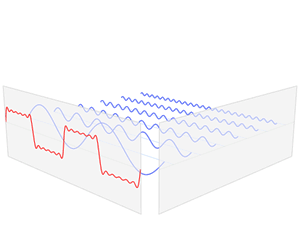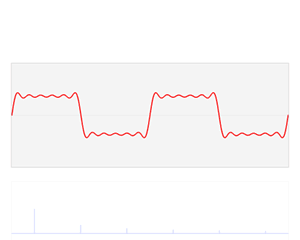
傅里叶级数的复数形式
复数形式可以由欧拉公式变化而来,只是简单的代入,不再赘述。
欧拉公式:
$$e^{it} = cos(t) + isin(t)$$
傅里叶复数:
$$f(x) = \sum_{-\infty}^{\infty}a_ke^{jk\omega\,t}$$
其中:
$$ak = \frac{1}{T}\int{-\frac{T}{2}}^{\frac{T}{2}}x(t)e^{-jk\omega\,t}dt$$
傅里叶变换
傅里叶级数有其局限性,只能用于周期函数,那么对于非周期函数怎么办呢?
对于非周期函数,我们可以这样思考,非周期看作周期无穷大,那么对应的$\omega$则无穷小,
傅里叶级数:
$$f(t) = \frac{1}{2\pi}\int{-\infty}^{\infty}F(\omega)e^{i\omega\,t}d\omega$$
其中:
$$F(\omega) = \int{-\infty}^{\infty}f(t)e^{-i\omega\,t}dt$$
注意,第二个公式才叫做 $f(x)$ 的傅里叶变换。更重要的是,这个式子里的角频率 $\omega$ 就不是某一个频点了,它可以取频谱轴上的任意值,它是连续的!非周期的信号的频谱遍布整个频率轴!
对某一点特定角频率 $\omega$ 取值,$F(\omega)$ 就是角频率 $\omega$ 在信号 $f(t)$ 中的”份量”!